S.2 Confidence Intervals

Allow's review the basic concept of a confidence interval.

Suppose nosotros want to estimate an actual population hateful \(\mu\). Every bit you lot know, we tin can simply obtain \(\bar{x}\), the mean of a sample randomly selected from the population of interest. Nosotros can use \(\bar{x}\) to detect a range of values:

\[\text{Lower value} < \text{population hateful}\;\; \mu < \text{Upper value}\]

that we tin be really confident contains the population mean \(\mu\). The range of values is called a "confidence interval."

Example Due south.2.ane

Should using a hand-held prison cell telephone while driving exist illegal? Section

There is little doubt that over the years you have seen numerous conviction intervals for population proportions reported in newspapers.

For example, a paper report (ABC News poll, May 16-20, 2001) was concerned whether or not U.Due south. adults thought using a hand-held cell phone while driving should be illegal. Of the 1,027 U.S. adults randomly selected for participation in the poll, 69% thought that information technology should be illegal. The reporter claimed that the poll's "margin of mistake" was three%. Therefore, the conviction interval for the (unknown) population proportion p is 69% ± 3%. That is, we can exist really confident that betwixt 66% and 72% of all U.South. adults remember using a hand-held cell phone while driving a car should exist illegal.

General Class of (Most) Conviction Intervals Department

The previous example illustrates the general form of well-nigh confidence intervals, namely:

$\text{Sample approximate} \pm \text{margin of error}$

The lower limit is obtained past:

$\text{the lower limit 50 of the interval} = \text{estimate} - \text{margin of error}$

The upper limit is obtained past:

$\text{the upper limit U of the interval} = \text{estimate} + \text{margin of mistake}$

Once we've obtained the interval, we can claim that we are actually confident that the value of the population parameter is somewhere between the value of L and the value of U.

So far, nosotros've been very general in our discussion of the calculation and estimation of confidence intervals. To be more specific about their use, let's consider a specific interval, namely the " t-interval for a population mean µ ."

(ane-α)100% t-interval for the population mean \(\mu\)

If we are interested in estimating a population mean \(\mu\), it is very probable that nosotros would use the t-interval for a population mean \(\mu\).

t-Interval for a Population Mean
The formula for the confidence interval in words is:

$\text{Sample mean} \pm (\text{t-multiplier} \times \text{standard mistake})$

and you lot might recall that the formula for the confidence interval in note is:
$\bar{x}\pm t_{\alpha/2, n-1}\left(\dfrac{s}{\sqrt{n}}\right)$

Note that:

  • the " t-multiplier," which we denote as \(t_{\blastoff/2, n-1}\), depends on the sample size through n - 1 (called the "degrees of liberty") and the confidence level \((1-\alpha)\times100%\) through \(\frac{\alpha}{2}\).
  • the "standard mistake," which is \(\frac{s}{\sqrt{due north}}\), quantifies how much the sample ways \(\bar{10}\) vary from sample to sample. That is, the standard mistake is just another proper noun for the estimated standard deviation of all the possible sample means.
  • the quantity to the right of the ± sign, i.east., " t -multiplier × standard error," is just a more specific form of the margin of fault. That is, the margin of fault in estimating a population mean µ is calculated by multiplying the t-multiplier by the standard error of the sample mean.
  • the formula is only advisable if a certain assumption is met, namely that the data are normally distributed.

Conspicuously, the sample mean \(\bar{x}\) , the sample standard deviation southward, and the sample size n are all readily obtained from the sample data. Now, we merely demand to review how to obtain the value of the t-multiplier, and nosotros'll exist all set.

How is the t-multiplier determined?

As the post-obit graph illustrates, nosotros put the confidence level $i-\alpha$ in the eye of the t-distribution. Then, since the entire probability represented by the curve must equal 1, a probability of α must exist shared equally amongst the two "tails" of the distribution. That is, the probability of the left tail is $\frac{\blastoff}{2}$ and the probability of the right tail is $\frac{\alpha}{2}$. If we add upward the probabilities of the various parts $(\frac{\alpha}{ii} + ane-\alpha + \frac{\alpha}{2})$, nosotros become ane. The t-multiplier, denoted \(t_{\alpha/2}\), is the t-value such that the probability "to the right of it" is $\frac{\alpha}{ii}$:

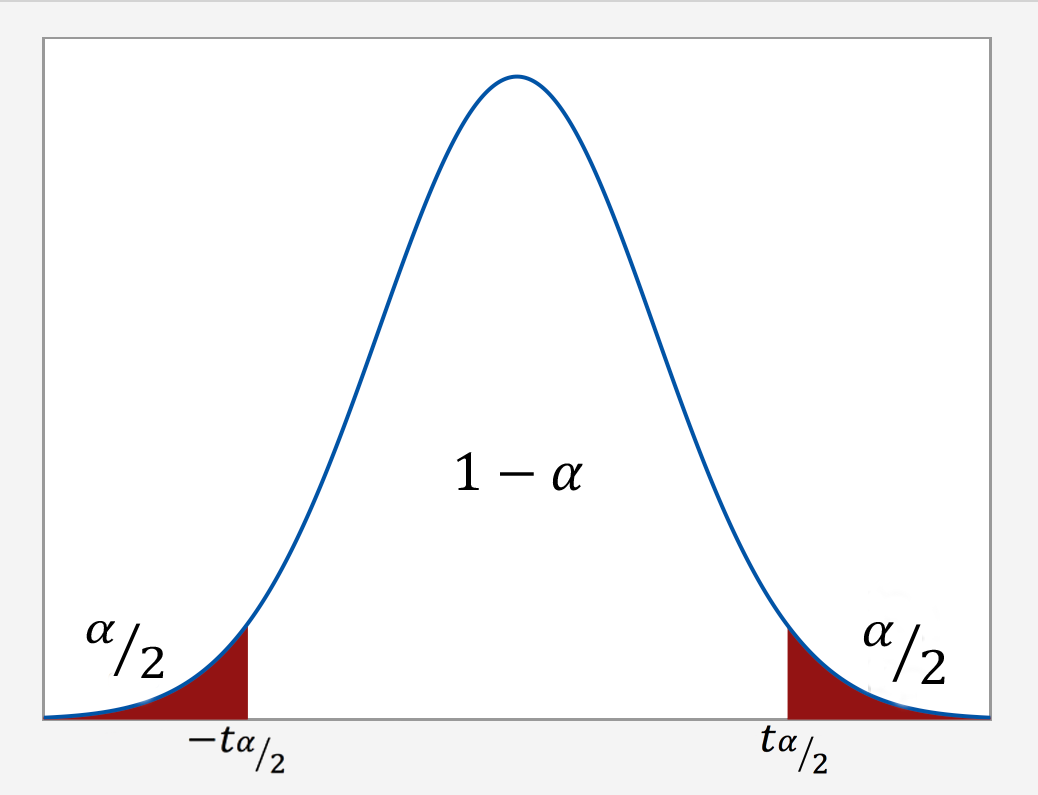
t-distribution

It should exist no surprise that we desire to be as confident as possible when we guess a population parameter. This is why conviction levels are typically very high. The nigh common confidence levels are xc%, 95% and 99%. The following table contains a summary of the values of \(\frac{\alpha}{2}\) corresponding to these common confidence levels. (Annotation that the"confidence coefficient" is merely the conviction level reported as a proportion rather than every bit a percentage.)

Conviction levels
Confidence Coefficient $(1-\blastoff)$ Confidence Level $(one-\alpha) \times 100$ $(1-\dfrac{\alpha}{2})$ $\dfrac{\alpha}{2}$
0.90 90% 0.95 0.05
0.95 95% 0.975 0.025
0.99 99% 0.995 0.005

Minitab 18

Minitab®  – Using Software

The skillful news is that statistical software, such equally Minitab, will calculate most confidence intervals for the states.

Let'southward accept an case of researchers who are interested in the average middle rate of male college students. Presume a random sample of 130 male college students were taken for the study.

The following is the Minitab Output of a ane-sample t-interval output using this data.

One-Sample T: Heart Rate

Descriptive Statistics
Due north Hateful StDev SE Mean 95% CI for $\mu$
130 73.762 7.062 0.619 (72.536, 74.987)

$\mu$: mean of Hour

In this example, the researchers were interested in estimating \(\mu\), the heart rate. The output indicates that the mean for the sample of n = 130 male students  equals 73.762. The sample standard difference (StDev) is 7.062 and the estimated standard error of the hateful (SE Mean) is 0.619. The 95% confidence interval for the population mean $\mu$ is (72.536, 74.987). We can be 95% confident that the hateful heart rate of all male college students is between 72.536 and 74.987 beats per minute.

Factors Affecting the Width of the t-interval for the Mean $\mu$ Section

Think nearly the width of the interval in the previous case. In general, do you think nosotros desire narrow confidence intervals or wide confidence intervals? If you are not certain, consider the post-obit ii intervals:

  • We are 95% confident that the average GPA of all college students is between ane.0 and 4.0.
  • We are 95% confident that the boilerplate GPA of all higher students is between 2.7 and ii.9.

Which of these two intervals is more than informative? Of course, the narrower one gives usa a ameliorate thought of the magnitude of the truthful unknown boilerplate GPA. In full general, the narrower the confidence interval, the more information we have virtually the value of the population parameter. Therefore, we want all of our confidence intervals to exist as narrow every bit possible. And so, let's investigate what factors impact the width of the t-interval for the mean \(\mu\).

Of course, to observe the width of the conviction interval, we just take the difference in the two limits:

Width = Upper Limit - Lower Limit

What factors touch the width of the confidence interval? We can examine this question by using the formula for the confidence interval and seeing what would happen should one of the elements of the formula exist immune to vary.

\[\bar{x}\pm t_{\alpha/2, n-1}\left(\dfrac{s}{\sqrt{n}}\right)\]

What is the width of the t-interval for the mean? If yous subtract the lower limit from the upper limit, you get:

\[\text{Width }=2 \times t_{\alpha/two, due north-ane}\left(\dfrac{s}{\sqrt{n}}\right)\]

Now, let's investigate the factors that affect the length of this interval. Convince yourself that each of the following statements is accurate:

  • Every bit the sample mean increases, the length stays the aforementioned. That is, the sample hateful plays no role in the width of the interval.
  • As the sample standard departure s decreases, the width of the interval decreases. Since s is an approximate of how much the data vary naturally, we have little control over southward other than making sure that we make our measurements as carefully as possible.
  • As we decrease the confidence level, the t-multiplier decreases, and hence the width of the interval decreases. In practice, we wouldn't want to set the confidence level beneath ninety%.
  • As nosotros increase the sample size, the width of the interval decreases. This is the cistron that nosotros take the nearly flexibility in changing, the just limitation beingness our time and financial constraints.

In Endmost

In our review of confidence intervals, nosotros accept focused on just one confidence interval. The important affair to recognize is that the topics discussed here — the general grade of intervals, determination of t-multipliers, and factors affecting the width of an interval — generally extend to all of the confidence intervals we will run across in this class.